Округлення натуральних чисел і десяткових дробів
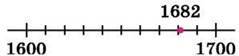
При округленні числа до заданого розряду необхідно, щоб округлене число якнайменше відрізнялося від заданого числа. Так, округлюючи 1682 до сотень, маємо 1682 ≈ 1700 (оскільки 1682 ближче до 1700, ніж до 1600)
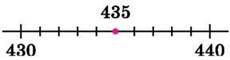
Нехай, наприклад, треба округлити до десятків число 435. Це особливий випадок, оскільки число 435 рівновіддалене від чисел 430 і 440 (рис. 256). У таких випадках домовилися округляти число “у більшу сторону”. Отже, 435 ≈ 440.
Маємо правило округлення натурального числа:
1) округлюючи натуральне число до певного розряду, всі цифри, що йдуть за ним, замінюють нулями;
2) якщо перша наступна за цим розрядом цифра 5, 6, 7, 8 або 9, то останню цифру, яка залишилася, збільшують на одиницю; якщо перша наступна за цим розрядом цифра 0, 1, 2, 3 або 4, то останню цифру, яка залишилася, не змінюють.
Приклад 1. Округли число 85 357 до тисяч.
Розв’язання. Підкреслимо цифру 5 у розряді тисяч: 85 357. Цифри, що стоять праворуч від неї (тобто 3, 5 та 7), замінюємо нулями. Наступна за розрядом тисяч є цифра 3, тому цифру тисяч 5 не змінюємо: 85 357 ≈ 85 000.
Відповідь: 85 000.
Приклад 2. Округли число 68 792 до найвищого розряду.
Розв’язання. Найвищим розрядом даного числа є десятки тисяч. Тому цифри 8, 7, 9 та 2 замінюємо нулями. Цифру в розряді десятків тисяч 6 збільшуємо на одиницю, оскільки наступна за нею цифра 8. Отже, записуємо так: 68 972 ≈ 70 000.
Відповідь: 70 000.
На практиці також часто виникає потреба округлити десяткові дроби. При цьому будемо користуватися тими самими правилами, що й для натуральних чисел.
Приклад 3. Округли число 82,2732 до десятих. Розв’язання. 82,2732 ≈ 82,3000. При цьому підкреслюємо цифру, що стоїть у розряді десятих. Цифри сотих, тисячних та десятитисячних замінюємо нулями, а цифру десятих збільшуємо на 1, оскільки наступною за нею є цифра 7. Проте 82,3000 = 82,3. Тому 82,2732 ≈ 82,3.
Приклад 4. Округли число 32,372 до сотих. Розв’язання. 32,372 ≈ 32,370. Підкреслюємо цифру, що стоїть у розряді сотих, цифру тисячних замінюємо нулем, а цифру сотих залишаємо без змін, оскільки наступною за нею є цифра 2. Проте 32,370 = 32,37. Тому 32,372 ≈ 32,37.
Приклад 5. Округли число 983,42 до десятків. Розв’язання. Якщо десятковий дріб округлюють до розряду, вищого за одиниці, то дробову частину відкидають, а цілу частину округлюють за правилом округлення натуральних чисел. Тому 983,42 ≈ 980. Отже, маємо правило округлення десяткового дробу:
Округлюючи десятковий дріб до певного розряду, 1) усі цифри, записані за цим розрядом, замінюємо нулями або відкидаємо (якщо вони стоять після коми); 2) якщо першою цифрою за цим розрядом є 0, 1, 2, 3 або 4, то останню цифру, що залишилася, не змінюємо; якщо першою цифрою за цим розрядом є 5, 6, 7, 8 або 9, то останню цифру, що залишилася, збільшуємо на 1.
Якщо при округленні десяткового дробу остання цифра, що залишилася в дробовій частині, буде 0, то відкидати її не можна (як ми це робимо з точними числами). У цьому разі цифра 0 наприкінці дробової частини показує, до якого розряду округлено число.

