УРОК " ГРАФІКИ ЗАЛЕЖНОСТЕЙ МІЖ ВЕЛИЧИНАМИ"


Зверніть увагу:
Усі точки графіка залежності прямо пропорційних величин лежать на одній прямій.
Ви знаете, що відстань і час на її подолання є прямопропорційними величинами. Тому всі точки графіка руху лежать на одній прямій.
Задача 1 . Потяг Харків – Львів вирушає з Харкова близько 19 год і прибуває до Львова близько 13 од. Швидкість потяга становить 50 км/год. На маршруті він робить 5 зупинок, які заплановано через кожні 3 години. На малюнку показано графік руху цього потяга.
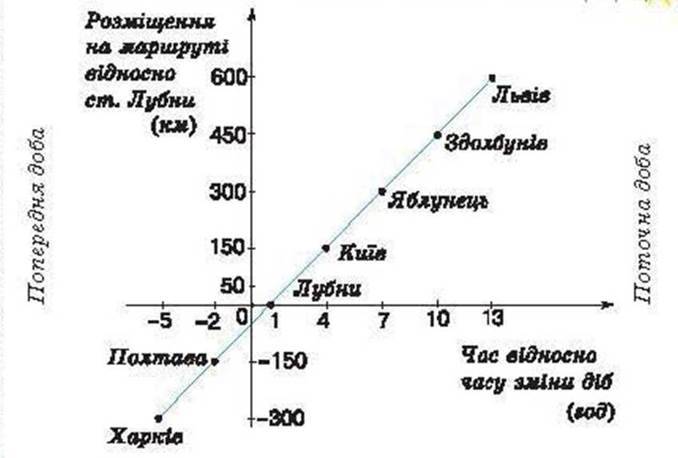
1) О котрій годині нової доби потяг робить першу зупинку? Яка це станція?
2) Що показує число -5 на осі абсцис? А число -2?
3) На яких відстанях від першої зупинки потяг зупиняється на інших станціях?
4) Що показує число -300 на осі ординат? а число -150?
5) Які координати кінцевих точок маршруту?
Розв’язання. За умовою задачі, рух потяга починається о 19 год, а завершується о 13 год наступного дня.
1. Початок нової доби потяг зустрічає недалеко від станції Лубни, а першу зупинку робить о 1 год саме на цій станції.
2. Оскільки рух потяга розпочався попередньої доби, то за віссю абсцис час його відправлення з Харкова можна виразити від’ємним числом -5. Справді, від 19 год попередньої доби до початку нової доби має пройти саме 5 год. Аналогічно, часові зупинки потяга в Полтаві на осі абсцис відповідає від’ємне число-2.
3. Зупинки заплановані через кожні 3 год. Оскільки швидкість потяга становить 50 км/год, то за 3 год він долає 150 км. Отже, потяг зупиняється на таких відстанях від Полтави: 150 км; 300 км; 450 км; 600 км; 750 км.
4. За допомогою від’ємних чисел-300 і-150 на осі ординат показано те, що о 19 год попередньої доби потяг перебував на відстані 3 00 км, не доїжджаючи до станції Лубни, а о 2 2 год попередньої доби – на відстані 150 км, не доїжджаючи до цієї станції.
5. Кінцеві точки маршруту потяга мають координати (-5; -300), (13; 600).
Чи обов’язково обирати кінцеві точки маршруту для побудови графіка руху? Ні. Графік можна побудувати за будь-якими двома його точками. Але кінці маршруту треба позначити неодмінно.
Зверніть увагу:
Графік руху є прямою (або її частиною), тому такий графік можна побудувати за будь-якими двом а його точками.
Дізнайтеся більше
За допомогою графіків можна розв’язувати цілий клас задач.
Розглянемо задачу.
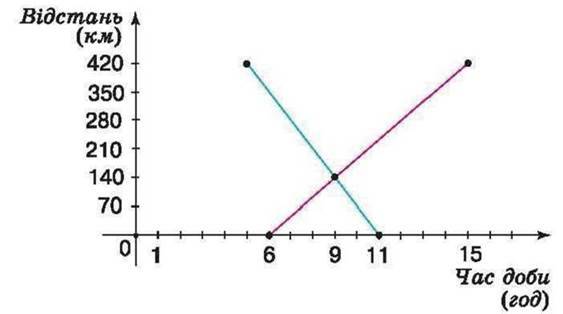
Задача 2. З пунктів А і В, відстань між якими становить 420 км, назустріч один одному виїхали два автомобілі. Червоний автомобіль виїхав о 6 год з пункту А і прибув у пункт В : о 15 год. Синій автомобіль виїхав о 5 год з пункту В і прибув у пункт А об 11 год. О котрій годині зустрінуться автомобілі?
Розв’язання. Побудуємо в прямокутній системі координат : графіки руху автомобілів. Червоний відрізок – графік руху червоного автомобіля, синій – синього автомобіля. Точці перетину цих відрізків відповідає час – 9 год. Отже, автомобілі зустрінуться о 9 год.
Урок "Координатна площина"

Проте на практиці часто доводиться користуватися орієнтирами не тільки вздовж прямої, а й на площині.
Ви знаєте, що у грі “Морський бій” положення корабля визначають за допомогою “координат” із цифр і “координат” із літер . Залежно від обраної букви пересуваються на певну кількість клітинок праворуч або ліворуч, а цифра вказує, на скільки клітинок треба зміститися вгору чи вниз. Отже, місце корабля на полі бою визначають двома “координатами”.
Щоб визначити місце в залі кінотеатру, теж треба знати дві “координати”: номер ряду та номер крісла в цьому ряді. Причому порядок “координат” у такій парі є строго визначеним. Справді, наприклад, пари чисел 3 і 12 та 12 і 3 спрямують нас у зовсім різні місця залу: в 3-й ряд на 12-те місце чи в 12-й ряд на 3-тє місце. На відміну від попереднього прикладу, для орієнтування в залі кінотеатру порядок координат не змінюють, незручно спочатку шукати номер місця в ряді, а лише потім – сам ряд.

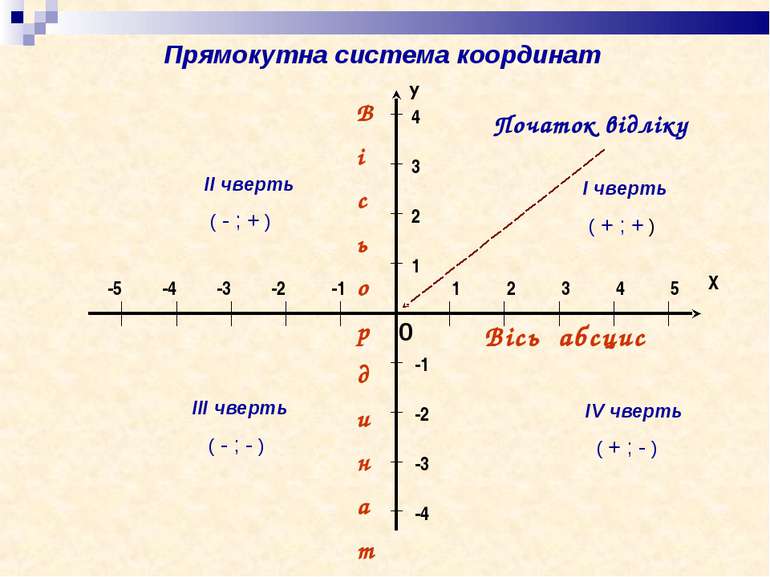
Отже, щоб охарактеризувати розміщення точки на площині, треба задати дві координатні прямі з рівними одиничними відрізками, одна з яких задає напрямок праворуч-ліворуч, а друга – вгору-вниз. Для цього координатні прямі зображають перпендикулярно одна до одної й так, щоб початки відліку на них збігалися. Одну із цих прямих (як правило горизонтальну) вважають першою, а іншу – другою. Така пара координатних прямих утворює прямокутну систему координат.
Першу координатну пряму називають віссю абсцис. Її позначають ОХ Другу координатну пряму називають віссю ординат. Її позначають OY. Спільний початок відліку координатних прямих називають початком координат .
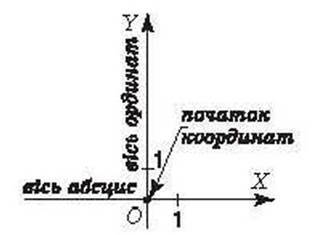
Площину з уведеною на ній системою координат називають координатною оскільки площиною.
Кожній точці на площині можна поставити у відповідність пару чисел, взятих у певному порядку, і навпаки, кожній парі чисел відповідає єдина точка координатної площини. Така упорядкована пара чисел називається координатами точки в даній системі координат. Координату за віссю абсцис називають абсцисою точки, а координату за віссю ординат – ординатою точки.
Коротко записують: М (х; у), А (В; 2). Читають: “Точка М з координатами х і у”, “Точка А з координатами В і 2” або “В – абсциса точки А, 2 – її ордината”.
Задача 1 . На координатній площині побудуйте точку:
1)5(3; 2); 2) А(5; 0).
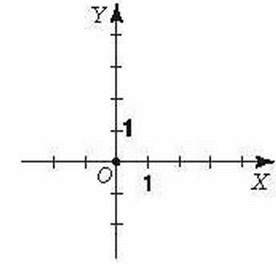
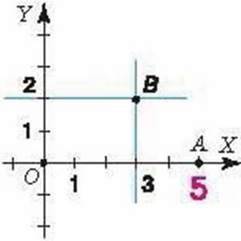
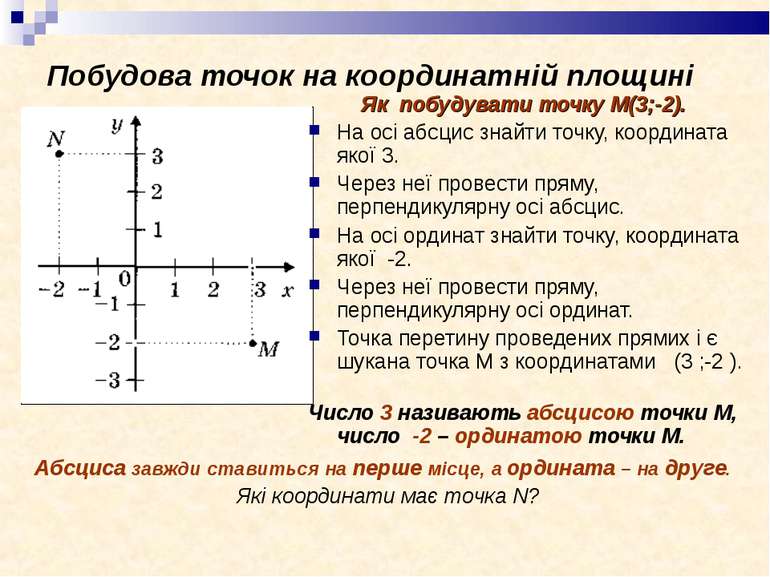
Розв’язання. Уведемо прямокутну систему координат на площині (мал. 167).
1. У точки В (3; 2) абсциса дорівнює З, а ордината – 2. На осі абсцис позначимо точку, що відповідає числу 3, а на осі ординат – точку, що відповідає числу 2. Через точки, побудовані на осях координат, проведемо дві прямі, паралельні осям (мал. 167). Точка перетину побудованих прямих – шукана точка В (3; 2).
2. Оскільки ордината точки А(5; 0) дорівнює 0, то ця точка лежить на осі абсцис і відповідає числу 5 на цій осі.
Зверніть увагу:
Точка лежить на осі абсцис, якщо її ордината дорівнює нулю, і навпаки;
Точка лежить на осі ординат, якщо її абсциса дорівнює нулю, і навпаки;
Початок координат – точка О, має координати (0; 0).
? Як визначити координати точки, побудованої на координатній площині, наприклад, точки А на малюнку 168? Для цього треба через дану точку провести прямі, паралельні осям координат.
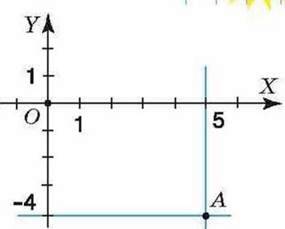
Пряма, паралельна осі ординат, перетинав вісь абсцис у точці, що відповідає числу 5.
Отже, першою координатою даної точки А є число 5. Пряма, паралельна осі абсцис, перетинав вісь ординат у точці, що відповідає числу -4. Отже, другою координатою точки А є число -4. Тоді точка А має координати 5 і -4, тобто А (5; -4).
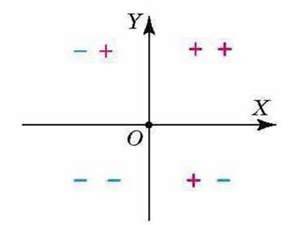
Координатні осі розбивають координатну площину на чотири частини. їх називають координатними чвертями і позначають так: І чверть, IIчверть, III чверть, IV чверть.
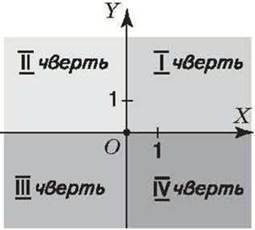
Точки І чверті мають додатну абсцису і додатну ординату. І навпаки, якщо абсциса й ордината точки додатні, то вона лежить у І чверті, як, наприклад, точка В (3; 2). Аналогічно міркуючи, можна з’ясувати, що точки II чверті мають від’ємну абсцису й додатну ординату, точки III чверті – від’ємну абсцису й від’ємну ординату, а точки IV чверті – додатну абсцису й від’ємну ординату.
На малюнку показано знаки координат точок, які лежать у відповідних чвертях.
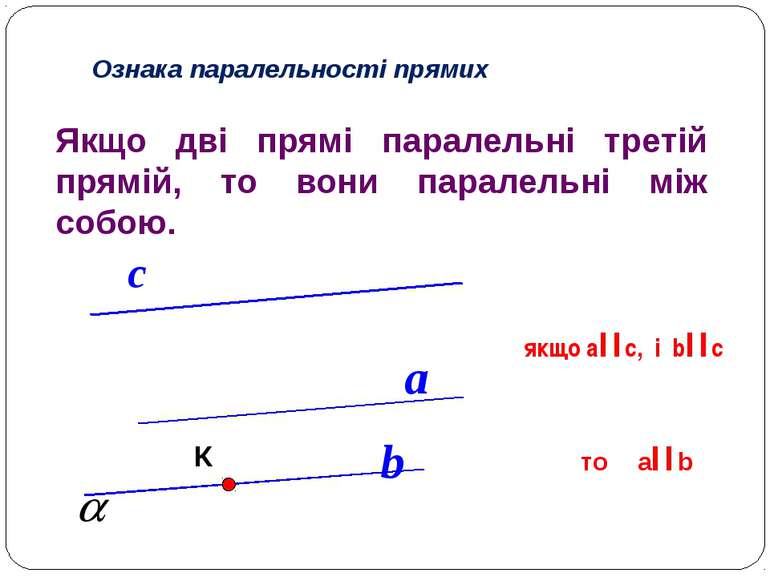
Урок "Паралельні прямі"



Цікавий приклад отримуємо, розглядаючи прямі на поверхні кулі (не на площині). Якщо куля досить велика, то в певній точці прямі можуть бути паралельними, але насправді вони перетинаються в точках, які називаються полюсами кулі.


Цей запис читають так: «Пряма AB паралельна прямій CD».
Інший спосіб для запису паралельних прямих — a || b.
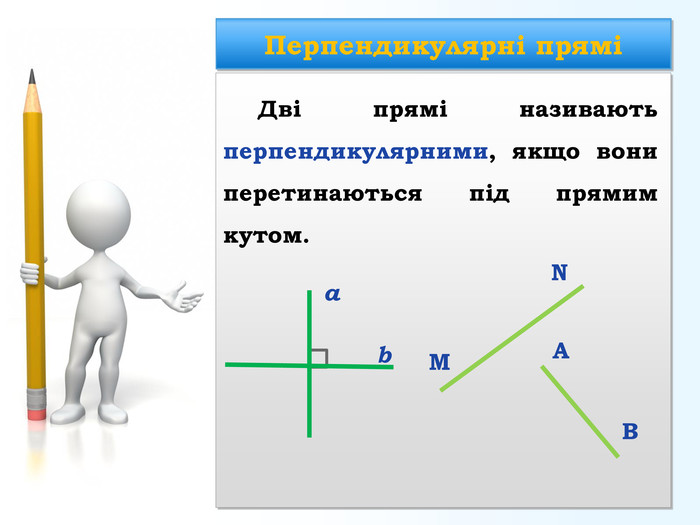
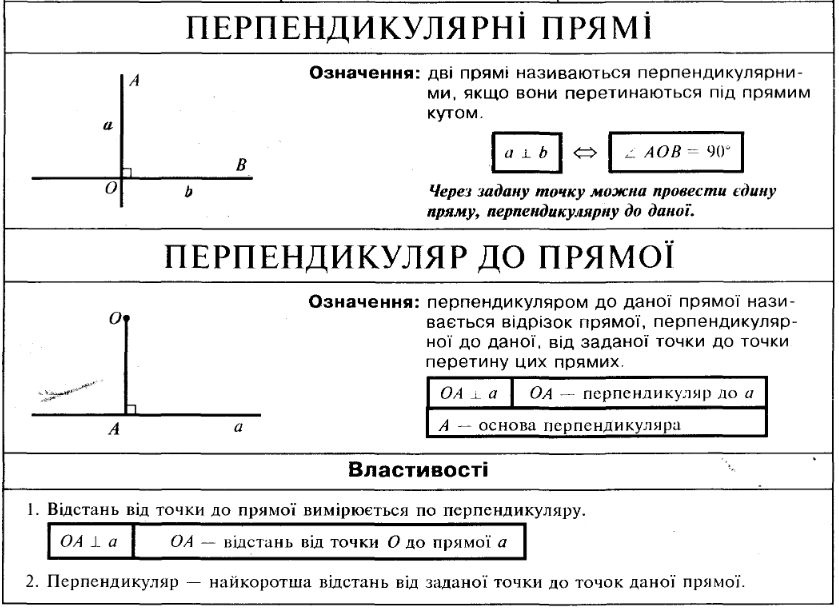
Урок "Перпендикулярні прямі"
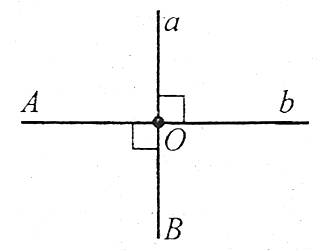
Означення. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
Наприклад: перпендикулярні прямі а і b (позначення ![]() , оскільки
, оскільки ![]() .
.
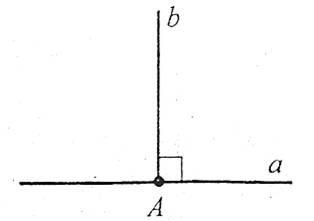
Теорема. Через кожну точку прямої можна провести перпендикулярну їй пряму, причому тільки одну.
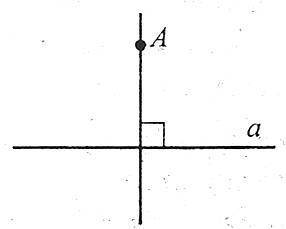
Теорема. Через дану точку поза прямою можна провести перпендикулярну даній пряму, причому тільки одну.
Розв’язування задач за допомогою рівнянь
Розглянемо приклади розв’язування текстових задач за допомогою рівнянь.
Задача 1. У двох кошиках разом 28 яблук, причому в другому на 4 яблука більше, ніж у першому. Скільки яблук у кожному кошику?
Розв’язання. Позначимо кількість яблук у першому кошику буквою x, тоді кількість яблук у другому буде (x + 4). Загальна кількість яблук x + (x + 4) за умовою задачі дорівнює 28. Маємо рівняння: X + (x + 4) = 28.
Розв’яжемо це рівняння:
x + x + 4 = 28,
2x = 28 –4,
2x = 24,
x = 24 : 2,
x = 12.
Отже, в першому кошику було 12 яблук, а в другому – 12 + 4 = 16 (яблук).
Перевірка. У другому кошику яблук на 4 більше, ніж у першому (16 – 12 = 4), в обох кошиках разом 28 яблук (12 + 16 = 28), що відповідає умові задачі.
Відповідь. 12 яблук у першому кошику, 16 яблук – у другому.
Розв’язавши задачу за допомогою рівняння, правильність її розв’язання треба перевірити за умовою задачі, а не за складеним рівнянням.
Отже, розв’язувати задачу за допомогою рівняння можна за таким планом:
1) позначаємо деяку невідому величину (число) буквою, наприклад, х;
2) інші невідомі величини виражаємо через цю букву;
3) виходячи з умови задачі, складаємо рівняння;
4) розв’язуємо це рівняння;
5) знаходимо інші невідомі величини, якщо цього вимагає умова задачі;
6) перевірка (необов’язково);
7) відповідь.
Задача 2. По трьох ящиках розклали 35 банок консервів так, що в першому ящику стало удвічі менше банок, ніж у другому, і на 3 менше, ніж у третьому. По скільки банок консервів стало в кожному ящику?
Розв’язання. Позначимо кількість банок консервів у першому ящику буквою x, тоді кількість банок у другому ящику – 2x, а в третьому – (x + 3). У трьох ящиках разом x + 2x + (x + 3) банок, що за умовою дорівнює 35. Маємо рівняння:
X + 2x + (x + 3) = 35.
Розв’яжемо його:
x + 2x + x + 3 = 35,
4x = 35 – 3,
4x = 32,
x = 32 : 4,
x = 8.
У першому ящику 8 банок, у другому – 2 ∙ 8 = 16 (банок), у третьому – 8 + 3 = 11 (банок).
Перевірку зробіть самостійно.
Відповідь. У першому ящику 8 банок, у другому – 16 банок, у третьому – 11 банок.
Розв'язування рівнянь. Основні властивості рівняння
Ви вже знаете, що таке рівняння, корінь рівняння. Пригадаємо основні формулювання.
Запам’ятайте !
Рівнянням називається рівність, що містить невідоме, значення якого треба знайти.
Невідоме число в рівнянні позначають буквою х, або у, або z тощо. Наприклад, запис 4х + 7 = 15 є рівнянням, де х – невідоме і є шуканим.
Значення невідомого, за якого рівняння перетворюється на правильну числову рівність, називається коренем рівняння.
Так, коренем рівняння 4х + 7 = 15 є число 2, бо 4-2 + 7 = 15.
Рівняння може мати більше, ніж один корінь. Наприклад, рівняння 0 ∙ х = 0 має безліч коренів, оскільки будь-яке число перетворюе рівняння на правильну числову рівність. З рівняннями, які мають два, три або більше коренів, ви зустрінетеся пізніше.
Рівняння може не мати коренів. Наприклад, рівняння 0 ∙ х = -12 не має коренів, бо не існує числа, яке в добутку з числом 0 дає число -12.
Розв’язати рівняння – означає знайти всі його корені або встановити, що рівняння не має жодного кореня.
У 5 класі ви ознайомились із найпростішими рівняннями. Розв’язуючи їх, ви знаходили корінь рівняння як невідомий компонент арифметичної дії. Під час розв’язування складніших рівнянь спираються на властивості рівностей. Розглянемо основні з них.
Поди віт вся на малюнок 1. Ви бачите, що на лівій шальці терезів розміщується кавун невідомої маси, а на правій – гирі масою 5 кг і 3 кг. Якщо на обидві шальки терезів покласти по гирі масою З кг, то терези залишаться в рівновазі (мал. ). Зрозуміло, що, знявши ці гирі або поставивши на терези однакові гирі іншої маси, знову дістанемо рівновагу на терезах. Цей приклад ілюструє таку властивість рівностей.
Запам’ятайте!
Якщо до обох частин рівності додати (від обох частин рівності відняти) одне й те саме число, то рівність не зміниться.
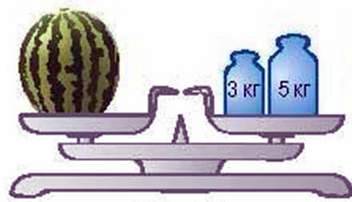
мал. 1
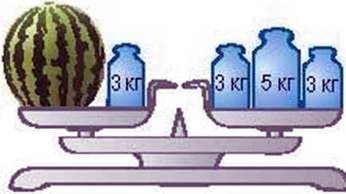
мал.2
Задача 1. Розв’яжіть рівняння: х – 12 = 20.
Розв’язання. До лівої і правої частий рівняння додамо число 12 і спростимо отриману рівність:
Х -12 = 20, х-12 + 12 = 20 + 12, х= 20 + 12, х= 32.
Розв’язуючи рівняння, у лівій його частині “усамітнили невідоме”. Такий самий результат отримаємо, якщо число 1 2 перенесемо з лівої частини у праву, змінивши при цьому його знак.
Запам’ятайте!
Доданок можна переносити з однієї частини рівняння в іншу, змінюючи знак цього доданка на протилежний? Чи можна переносити до іншої частини рівняння доданок, що містить невідоме? Так.
Подивіться на малюнок 3. Ви бачите, що маса пакета борошна дорівнює 2 кг. Зрозуміло, що маса трьох таких пакетів утричі більша (мал. 4). Цей приклад ілюструє іншу властивість рівностей.
Запам’ятайте!
Якщо обидві частини рівності помножити (поділити) на одно й то само число, відмінно від нуля, то рівність не зміниться.
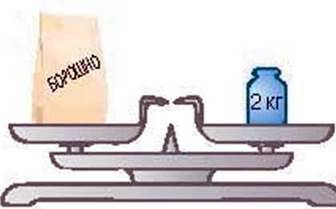
мал.3
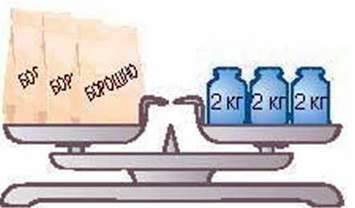
мал.4
Наведену властивіств використовують для розв’язування рівнянь. Розглянемо приклад.
Задача 9 Розв’яжіть рівняння 
Розв’язання. Щоб позбутися дробового коефіцієнта, помножимо на 3 обидві частини рівняння:

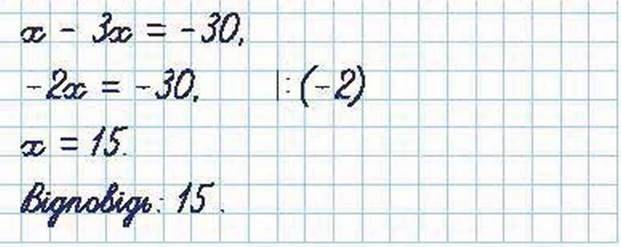
Запам’ятайте!
Основні властивості рівнянь
1. Корені рівняння не зміняться, якщо до обох частин рівняння додати (від обох частин рівняння відняти) одне й те саме число.
2. Корені рівняння не зміняться, якщо обидві частини рівняння помножити (поділити) на одне й те саме число, відмінне від нуля.

Ділення раціональних чисел
Ви знаєте, що для додатних чисел дію ділення можна звести до дії множення на число, обернене до дільника.
Нехай треба поділити число 20 на число  Це означає, що число 20 можна помножити на число, обернене до числа
Це означає, що число 20 можна помножити на число, обернене до числа  тобто на число
тобто на число 

Тоді, за правилом множення чисел з різними знаками, дістанемо:

Отже, 
Бачимо, що частка чисел 20 і 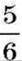 дорівнює частці їх модулів, узятій зі знаком “-“:
дорівнює частці їх модулів, узятій зі знаком “-“:

Частка чисел -20 та  дорівнює частці їх модулів, узятій зі знаком “-“:
дорівнює частці їх модулів, узятій зі знаком “-“:

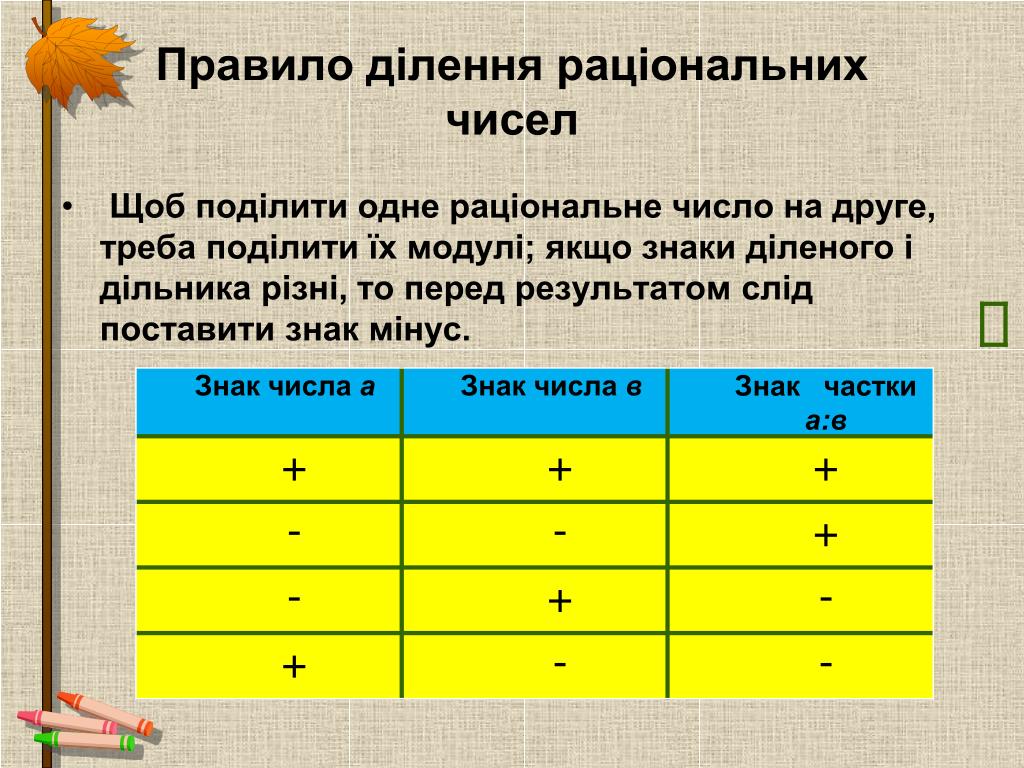
Запам’ятайте!
Правило ділення чисел з різними знаками Частка двох чисел з різними знаками – число від’ємне. Щоб знайти частку чисел з різними знаками, треба поділити модуль діленого на модуль дільника і перед отриманою часткою поставити знак “-“.
Як поділити одне від’ємне число на інше? Міркуючи аналогічно до попереднього випадку, для чисел -20 і  дістанемо:
дістанемо:

Запам’ятайте!
Правило ділення двох від’ємних чисел Частка двох від’ємних чисел – число додатне.
Щоб знайти частку двох від’ємних чисел, достатньо поділити модуль діленого на модуль дільника.
Узагалі, знак частки раціональних чисел визначається знаками діленого і дільника. Наприклад:
4 = 8:2 або 4 = -8: (-2);
-4 = -8 : 2 або -4 = 8: (-2).
Якщо число 0 поділити на будь-яке раціональне число, відмінне від нуля, то в частці дістанемо 0: 0 : а = 0 для а ≠ 0.
Дія ділення на 0 не має змісту і для раціональних чисел. Тому: на 0 ділити не можна!
Зверніть увагу:
– у частці а : b число b не може дорівнювати нулю;
– якщо частка а : b додатна, то числа а і b мають однакові знаки, і навпаки;
– якщо частка а : b від’ємна, то числа а і b мають різні знаки, і навпаки;
– якщо частка а : b дорівнює нулю, то а дорівнює нулю, і навпаки.
Оскільки а ∙ 1 = а, то а : 1 = а для будь-якого а, і а : а = 1 для а ≠ 0.
Якщо число, відмінне від нуля, поділити на -1, то в частці дістанемо протилежне до нього число.
Наприклад, 5 : (-1) = -5.
Частка двох протилежних чисел, відмінних від нуля, дорівнює -1: – а : а = а : (-а) = -1 для а ≠ 0.
Розподільна властивість множення. Зведення подібних доданків
Розподільна властивість множення дає можливість виносити спільний множник за дужки.
Приклад 1. Спрости вираз 7x – 6x + 3x.
Розв’язання. Усі доданки мають спільний множник х. Маємо: 7x – 6x + 3x = (7 – 6 + 3) ∙ х. У дужках записано суму коефіцієнтів усіх доданків, вона дорівнює 4.
Тому 7x – 6x + 3x = 4x.
У виразі 7x – 6x + 3x доданки 7x, -6x, 3x мають спільну буквену частину і відрізняються один від одного лише коефіцієнтами. Такі доданки називають подібними.
Доданки, що мають однакову буквену частину, називають подібними доданками.
Додавання подібних доданків називають зведенням подібних доданків.
– Щоб звести подібні доданки, достатньо додати їх коефіцієнти і знайдений результат помножити на спільну буквену частину.
Приклад 2. Звести подібні доданки: 1) 4а + а – 6а; 2) 7b – 3b – 4b.
Розв’язання. 1)У цьому прикладі всі доданки подібні, оскільки в них спільна частина а. Додаючи коефіцієнти, маємо: 4 + 1 – 6 = -1. Отже, 4а + а – 6а = -1 ∙ а = – а; 2) 7b – 3b – 4b = 0 ∙ b = 0.
Вираз може містити доданки з різними буквеними частинами. Тоді доданки можна об’єднати у групи з однаковою буквеною частиною. Доданки з різних груп доцільно підкреслювати по-різному.
Приклад 3. Спростити вираз 4а + 5b – 7а + 4 + 3b.
Розв’язання.
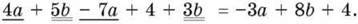
Приклад 4. Розв’язати рівняння 4(x + 2) – (x – 2) = 13.
Розв’язання.
Розкриємо дужки: 4x + 8 – x + 2 = 13.
Зведемо подібні доданки 3x + 10 = 13.
Далі 3x = 13 – 10;
3x = 3;
x = 3 : 3;
x = 1.


Переставна і сполучна властивості множення. Коефіцієнт буквенного виразу.
Для множення раціональних чисел, як і для множення додатних чисел, справджуються переставна і сполучна властивості.
Переставна властивість множення.
– Для будь-яких раціональних чисел а і b виконується рівність ab = ba.
Перевіримо цю властивість на прикладах.
Приклад 1. -3 ∙ 2 = -6; 2 ∙ (-3) = -6, тому -3 ∙ 2 = = 2 ∙ (-3).
Приклад 2. -4 ∙ (-7) = 28; -7 ∙ (-4) = 28, тому -4 ∙ (-7) = = -7 ∙ (-4).
Сполучна властивість множення.
– Для будь-яких раціональних чисел а, b і c виконується рівність (ab)c = a(bc).
Перевіримо цю властивість на прикладі.
Приклад 3. (-2 ∙ 3) ∙ (-4) = -6 ∙ (-4) = 24; -2 ∙ (3 ∙ (-4)) = = -2 ∙ (-12) = 24, тому (-2 ∙ 3) ∙ (-4) = -2 ∙ (3  (-4)).
(-4)).
Зауважимо також, що для будь-якого раціонального числа а виконуються рівності:
А ∙ 1 =1 ∙ а = а; а ∙ (-1) = -1 ∙ а = – а; а 0 = 0 а = 0.
Властивості множення дають можливість спростити процес обчислення добутку кількох множників, обираючи зручний порядок обчислень.
Приклад 4.
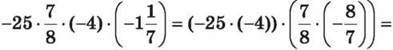 100 ∙ (-1) = -100.
100 ∙ (-1) = -100.Зауважимо, що добуток кількох чисел, відмінних від нуля, – число від’ємне, якщо кількість від’ємних множників непарна. Якщо кількість від’ємних множників парна, то добуток – число додатне. Добуток дорівнює нулю, якщо хоча б один із множників дорівнює нулю.
Властивості множення дають можливість спрощувати вирази.
Приклад 5. Спростити вираз -2а ∙ 3b ∙ (-5).
Розв’язання. -2а ∙ 3b ∙ (-5) = -2 ∙ а ∙ 3 ∙ b ∙ (-5) = (-2 ∙ 3 ∙ (-5)) ∙ (а ∙ b) = 30аb.
Число 30 називають коефіцієнтом отриманого буквеного виразу 30аb. Наприклад, вираз -4х має коефіцієнт -4.
– Якщо вираз є добутком числа і однієї або кількох букв, то це число називають числовим коефіцієнтом (або просто коефіцієнтом).
Зазвичай коефіцієнт записують перед буквеним множником, а коефіцієнт 1 не пишуть. Отже, 1 ∙ mn = mn, буквений вираз mn має коефіцієнт 1. Замість коефіцієнта -1 пишуть тільки знак “-“. Наприклад, замість -1 ∙ xy пишуть – xу, тобто -1 ∙ xy = – xу, буквений вираз – xy має коефіцієнт -1.

Множення раціональних чисел
Дії з цілими числами мають такі ж властивості дій, як і з натуральними числами. Тобто, дії з раціональними числами мають властивості дій з цілими числами. Але при множенні раціональних чисел є ще додаткове властивість множення взаємно обернених чисел.
Щоб помножити 2 раціональних числа, потрібно помножити модулі цих чисел і перед відповіддю поставити знак «+», коли у множників однакові знаки, або «-», коли у множників різні знаки.
Приклад:
(-2) · (-3) = +6; (-0,5) · (+2) = -1;
(+2) · (+4) = +8; (+0,5) · (-4) = -2.
Множення раціональних чисел на нуль. Коли хоч 1 множник це нуль, то і твір буде нулем.
Приклад:
0 · (-5) = 0; (+2,5) · 0 = 0.
Множення раціональних чисел з різними знаками. Для множення кілька чисел з різними знаками, потрібно помножити модулі кожного числа і обчислити знак результату: коли кількість множників з негативними знаками парне, то твір стане зі знаком «+», коли кількість множників з негативними знаками непарне, то твір стане зі знаком «-».
Приклад:
(-5) · (+4) · (-2) · (-3) · (+10) = -1200 (кількість від’ємних множників непарне – 3).
(+2,5) · (-7,3) · (+ 4) · (-2) · (-1) · (+4) · (-0,5) = +292 (кількість від’ємних множників парне – 4).
Множення раціональних чисел на 1: результатом множення будь-якого раціонального числа a на 1 буде a. Тобто, a·1=a 1·a=a, для будь-якого раціонального числа a. Т. о., одиниця – це нейтральне числом по множенню.
Множення взаємно зворотних раціональних чисел. Коли множники – це взаємно обернені числа, значить їх твір одиниця. Тобто, a·a−1=1.
Таким чином, якщо помножити такі взаємнооборотні числа, як: 7/8 і 8/7 отримаємо одиницю. Аналогічно, множення -1,5 на -0,(6) у результаті буде 1, т. к. -1,5=-3/2 і -0,(6)=-2/3, а -3/2 і -2/3 – взаємно обернені числа.

Розкриття дужок
Згадаємо, як до числа а додати суму чисел b і c. Можна спочатку до а додати b, а потім до отриманого результату додати c:
А + (b + c) = а + b + c.
Ми записали вираз а + (b + c) без дужок. Таке перетворення виразу називають розкриттям дужок.
Приклад 1. Розкрити дужки у виразі а + (b – c).
Розв’язання. а + (b – c) = а + (b + (-c)) = а + b + (-c) = а + b – c.
Приклад 2. Розкрити дужки у виразі а + (-b – c).
Розв’язання. а + (-b – c) = а + ((-b) + (-c)) = а + (-b) + (-c) = а – b – c.
Вираз а + b – c можна отримати з виразу а + (b – c), а вираз а – b – c з виразу а + (-b – c), якщо не писати дужки та знак “+” та записати всі доданки, які були в дужках, зі своїми знаками. Маємо правило розкриття дужок, перед якими стоїть знак “+”:
– щоб розкрити дужки, перед якими стоїть знак “+”, треба не писати дужки і знак “+”, що стоїть перед ними, та записати всі доданки зі своїми знаками.
Приклад 3. Розкрити дужки і знайти значення виразу 5,2 + (-7,2 + 3).
Розв’язання. 5,2 + (-7,2 + 3) = 5,2 – 7,2 + 3 = 1.
Згадаємо і запишемо правило віднімання від числа а суми чисел b і с: а – (b + с) = а – b – с.
Ми записали вираз а – (b + с) без дужок. Розглянемо ще приклад розкриття дужок, перед якими стоїть знак “-“.
Приклад 4. Розкрити дужки у виразі а – (b – с).
Розв’язання. а – (b – с) = а – (b + (-с)) = а – b – (-с) = а – b + с.
Вираз а – b – с можна отримати з виразу а – (b + с), а вираз а – b + с – з виразу а – (b – с), якщо не писати дужки і знак “-” та записати всі доданки, які були в дужках, з протилежними знаками. Маємо правило розкриття дужок, перед якими стоїть знак “-“:
– щоб розкрити дужки, перед якими стоїть знак “-“, треба не писати дужки і знак “-“, що стоїть перед ними, та записати всі доданки з протилежними знаками.
Приклад 5. Розкрити дужки і знайти значення виразу -4,9 – (5,2 – 8,1).
Розв’язання. -4,9 – (5,2 – 8,1) = -4,9 – 5,2 + 8,1 = -10,1 + 8,1 = -2.
Приклад 6. Спростити вираз:
1) 7 – (а – 8); 2) (x – 5) – (x + 8).
Розв’язання. 1) 7 – (а – 8) = 7 – а + 8 = (7 + 8) – а = 15 – а.
2) Як відомо, при запису додатних чисел знак “+”, як правило, не пишуть. Так само знак “+” не пишуть на початку прикладу перед дужками. Отже, замість + (x – 5) пишуть (x – 5). Маємо:
(x – 5) – (x + 8) = x – 5 – x – 8 = х + (-х) + (-5 – 8) = = 0 + (-13) = -13.

Додавання та віднімання чисел із різними знаками
Додавання від’ємних чисел:
-a+(-b)=-a-b=-(a+b),
де a і b – додатні числа.
Наприклад: -5-3=-8.
Додавання чисел із різними знаками:
-a+b=-(a-b)
Наприклад: -10+2=-(10-2)=-8.
-b+a=a-b
Наприклад: -3+10=10-3=7.
Віднімання додатних і від’ємних чисел
Відняти від числа a число b означає додати до числа a число, протилежне b:
a-b=a+(-b)
Наприклад: 5-6=5+(-6)=1; -3-(-5)=-3+5=2.

УРОК № 2 "Порівняння раціональних чисел"
Порівняємо числа 9, -4 і -2,5 за допомогою координатної прямої. Для цього позначимо на ній точки А, В і С, що відповідають цим числам. Як бачимо, правіше від усіх розміщена точка А (9). Отже, число 9 є найбільшим. Лівіше від усіх розміщена точка В(-4), тому число -4 є найменшим. Можемо записати дані числа в порядку зростання: -4: -2,5; 9.
Запам’ятайте!
1. Порівняти два раціональні числа – означає встановити, яке з них є більшим, а яке – меншим.
2. із двох раціональних чисел більшим є те число, для якого відповідна точка на координатній прямій розміщується правіше.
Результат порівняння раціональних чисел записують за допомогою числових нерівностей. Наприклад, -4 <9; 9 >-2,5; -4 <-2,5 <9.
Задача 1 . Які Цілі числа більші за -5 і менші від 6,8?
Розв’язання. Позначимо точки А (-5) і В (6,8) на координатній прямій (мал. 119). На ній шукані числа розміщуються між координатами точок А і В. Це числа -4, -3, -2, -1, 0,1, 2,3,4, 5,6.

Яку закономірність помічаємо, порівнюючи з числом -5 від? ємні числа -4, – З, -2, -1? Числа від -5 до -1 збільшуються, але їх модулі зменшуються. Для додатних чисел 1, 2, З, 4, 5, 6 закономірність інша – і числа збільшуються, і їх модулі збільшуються. Число 0 залишається більшим за кожне від’ємне число, але меншим від кожного додатного числа.
Можемо сформулювати правила порівняння раціональних чисел. Користуючись ними для порівняння чисел, не обов’язково будувати координатну пряму.
Запам’ятайте!
Правила порівняння раціональних чисел
1. Від’ємне число завжди менше від додатного числа.
2. Число 0 менше від додатного числа, але більше за від’ємне число.
3. Із двох додатних чисел більшим є те число, модуль якого більший.
4. Із двох від’ємних чисел більшим є те число, модуль якого менший.
Якщо число а додатне, то записують: а > 0.
Якщо число а від’ємне, то записують: а < 0.
Якщо число а недодатне, то записують: а < 0.
Якщо число а невід’ємне, то записують: а > 0.
? Чи правильно, що будь-яке раціональне число завжди більше за протилежне до нього число? Ні. Наприклад, для числа-5 протилежним є число 5, але -5 < 5.
Зверніть увагу:
Щоб спростувати деяке твердження, достатньо одного прикладу.
УРОК № 1 "МОДУЛЬ ЧИСЛА"
Протилежні числа мають рівні модулі:
