Переставна і сполучна властивості множення. Коефіцієнт буквенного виразу.
Для множення раціональних чисел, як і для множення додатних чисел, справджуються переставна і сполучна властивості.
Переставна властивість множення.
– Для будь-яких раціональних чисел а і b виконується рівність ab = ba.
Перевіримо цю властивість на прикладах.
Приклад 1. -3 ∙ 2 = -6; 2 ∙ (-3) = -6, тому -3 ∙ 2 = = 2 ∙ (-3).
Приклад 2. -4 ∙ (-7) = 28; -7 ∙ (-4) = 28, тому -4 ∙ (-7) = = -7 ∙ (-4).
Сполучна властивість множення.
– Для будь-яких раціональних чисел а, b і c виконується рівність (ab)c = a(bc).
Перевіримо цю властивість на прикладі.
Приклад 3. (-2 ∙ 3) ∙ (-4) = -6 ∙ (-4) = 24; -2 ∙ (3 ∙ (-4)) = = -2 ∙ (-12) = 24, тому (-2 ∙ 3) ∙ (-4) = -2 ∙ (3 
(-4)).
Зауважимо також, що для будь-якого раціонального числа а виконуються рівності:
А ∙ 1 =1 ∙ а = а; а ∙ (-1) = -1 ∙ а = – а; а 0 = 0 а = 0.
Властивості множення дають можливість спростити процес обчислення добутку кількох множників, обираючи зручний порядок обчислень.
Приклад 4.
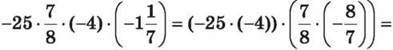100 ∙ (-1) = -100.Зауважимо, що добуток кількох чисел, відмінних від нуля, – число від’ємне, якщо кількість від’ємних множників непарна. Якщо кількість від’ємних множників парна, то добуток – число додатне. Добуток дорівнює нулю, якщо хоча б один із множників дорівнює нулю.
Властивості множення дають можливість спрощувати вирази.
Приклад 5. Спростити вираз -2а ∙ 3b ∙ (-5).
Розв’язання. -2а ∙ 3b ∙ (-5) = -2 ∙ а ∙ 3 ∙ b ∙ (-5) = (-2 ∙ 3 ∙ (-5)) ∙ (а ∙ b) = 30аb.
Число 30 називають коефіцієнтом отриманого буквеного виразу 30аb. Наприклад, вираз -4х має коефіцієнт -4.
– Якщо вираз є добутком числа і однієї або кількох букв, то це число називають числовим коефіцієнтом (або просто коефіцієнтом).
Зазвичай коефіцієнт записують перед буквеним множником, а коефіцієнт 1 не пишуть. Отже, 1 ∙ mn = mn, буквений вираз mn має коефіцієнт 1. Замість коефіцієнта -1 пишуть тільки знак “-“. Наприклад, замість -1 ∙ xy пишуть – xу, тобто -1 ∙ xy = – xу, буквений вираз – xy має коефіцієнт -1.
