УРОК № 2 "Порівняння раціональних чисел"
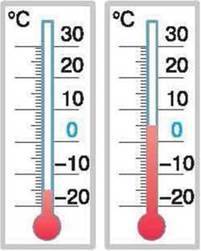
Порівняємо числа 9, -4 і -2,5 за допомогою координатної прямої. Для цього позначимо на ній точки А, В і С, що відповідають цим числам. Як бачимо, правіше від усіх розміщена точка А (9). Отже, число 9 є найбільшим. Лівіше від усіх розміщена точка В(-4), тому число -4 є найменшим. Можемо записати дані числа в порядку зростання: -4: -2,5; 9.
Запам’ятайте!
1. Порівняти два раціональні числа – означає встановити, яке з них є більшим, а яке – меншим.
2. із двох раціональних чисел більшим є те число, для якого відповідна точка на координатній прямій розміщується правіше.
Результат порівняння раціональних чисел записують за допомогою числових нерівностей. Наприклад, -4 <9; 9 >-2,5; -4 <-2,5 <9.
Задача 1 . Які Цілі числа більші за -5 і менші від 6,8?
Розв’язання. Позначимо точки А (-5) і В (6,8) на координатній прямій (мал. 119). На ній шукані числа розміщуються між координатами точок А і В. Це числа -4, -3, -2, -1, 0,1, 2,3,4, 5,6.

Яку закономірність помічаємо, порівнюючи з числом -5 від? ємні числа -4, – З, -2, -1? Числа від -5 до -1 збільшуються, але їх модулі зменшуються. Для додатних чисел 1, 2, З, 4, 5, 6 закономірність інша – і числа збільшуються, і їх модулі збільшуються. Число 0 залишається більшим за кожне від’ємне число, але меншим від кожного додатного числа.
Можемо сформулювати правила порівняння раціональних чисел. Користуючись ними для порівняння чисел, не обов’язково будувати координатну пряму.
Запам’ятайте!
Правила порівняння раціональних чисел
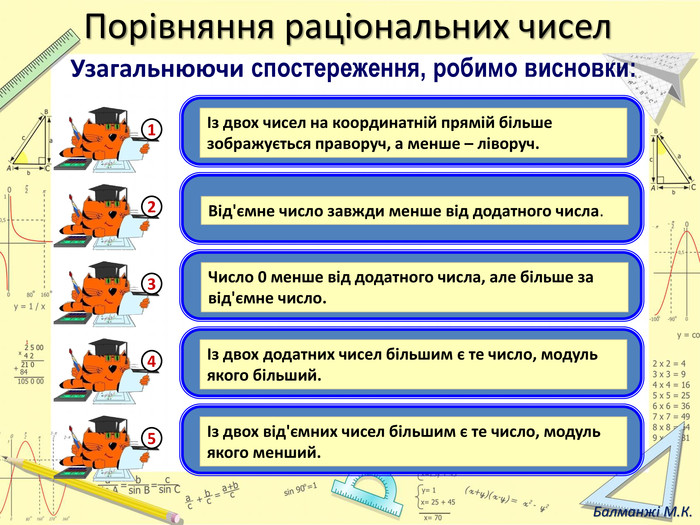
1. Від’ємне число завжди менше від додатного числа.
2. Число 0 менше від додатного числа, але більше за від’ємне число.
3. Із двох додатних чисел більшим є те число, модуль якого більший.
4. Із двох від’ємних чисел більшим є те число, модуль якого менший.
Якщо число а додатне, то записують: а > 0.
Якщо число а від’ємне, то записують: а < 0.
Якщо число а недодатне, то записують: а < 0.
Якщо число а невід’ємне, то записують: а > 0.
? Чи правильно, що будь-яке раціональне число завжди більше за протилежне до нього число? Ні. Наприклад, для числа-5 протилежним є число 5, але -5 < 5.
Зверніть увагу:
Щоб спростувати деяке твердження, достатньо одного прикладу.