Розподільна властивість множення. Зведення подібних доданків
Розподільна властивість множення дає можливість виносити спільний множник за дужки.
Приклад 1. Спрости вираз 7x – 6x + 3x.
Розв’язання. Усі доданки мають спільний множник х. Маємо: 7x – 6x + 3x = (7 – 6 + 3) ∙ х. У дужках записано суму коефіцієнтів усіх доданків, вона дорівнює 4.
Тому 7x – 6x + 3x = 4x.
У виразі 7x – 6x + 3x доданки 7x, -6x, 3x мають спільну буквену частину і відрізняються один від одного лише коефіцієнтами. Такі доданки називають подібними.
Доданки, що мають однакову буквену частину, називають подібними доданками.
Додавання подібних доданків називають зведенням подібних доданків.
– Щоб звести подібні доданки, достатньо додати їх коефіцієнти і знайдений результат помножити на спільну буквену частину.
Приклад 2. Звести подібні доданки: 1) 4а + а – 6а; 2) 7b – 3b – 4b.
Розв’язання. 1)У цьому прикладі всі доданки подібні, оскільки в них спільна частина а. Додаючи коефіцієнти, маємо: 4 + 1 – 6 = -1. Отже, 4а + а – 6а = -1 ∙ а = – а; 2) 7b – 3b – 4b = 0 ∙ b = 0.
Вираз може містити доданки з різними буквеними частинами. Тоді доданки можна об’єднати у групи з однаковою буквеною частиною. Доданки з різних груп доцільно підкреслювати по-різному.
Приклад 3. Спростити вираз 4а + 5b – 7а + 4 + 3b.
Розв’язання.
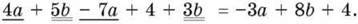
Приклад 4. Розв’язати рівняння 4(x + 2) – (x – 2) = 13.
Розв’язання.
Розкриємо дужки: 4x + 8 – x + 2 = 13.
Зведемо подібні доданки 3x + 10 = 13.
Далі 3x = 13 – 10;
3x = 3;
x = 3 : 3;
x = 1.

