Ділення раціональних чисел
Ви знаєте, що для додатних чисел дію ділення можна звести до дії множення на число, обернене до дільника.
Нехай треба поділити число 20 на число 
Це означає, що число 20 можна помножити на число, обернене до числа 
тобто на число 
Тоді, за правилом множення чисел з різними знаками, дістанемо:
Отже, 
Бачимо, що частка чисел 20 і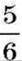 
дорівнює частці їх модулів, узятій зі знаком “-“:
Частка чисел -20 та 
дорівнює частці їх модулів, узятій зі знаком “-“:
Запам’ятайте!
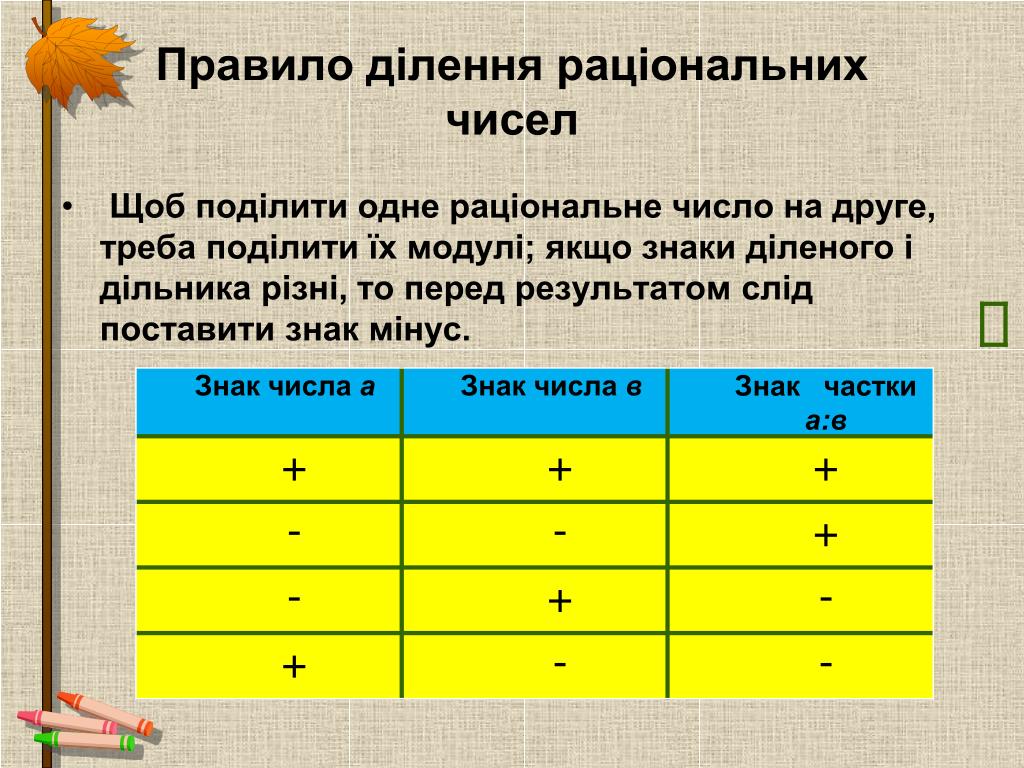
Правило ділення чисел з різними знаками Частка двох чисел з різними знаками – число від’ємне. Щоб знайти частку чисел з різними знаками, треба поділити модуль діленого на модуль дільника і перед отриманою часткою поставити знак “-“.
Як поділити одне від’ємне число на інше? Міркуючи аналогічно до попереднього випадку, для чисел -20 і 
дістанемо:
Запам’ятайте!
Правило ділення двох від’ємних чисел Частка двох від’ємних чисел – число додатне.
Щоб знайти частку двох від’ємних чисел, достатньо поділити модуль діленого на модуль дільника.
Узагалі, знак частки раціональних чисел визначається знаками діленого і дільника. Наприклад:
4 = 8:2 або 4 = -8: (-2);
-4 = -8 : 2 або -4 = 8: (-2).
Якщо число 0 поділити на будь-яке раціональне число, відмінне від нуля, то в частці дістанемо 0: 0 : а = 0 для а ≠ 0.
Дія ділення на 0 не має змісту і для раціональних чисел. Тому: на 0 ділити не можна!
Зверніть увагу:
– у частці а : b число b не може дорівнювати нулю;
– якщо частка а : b додатна, то числа а і b мають однакові знаки, і навпаки;
– якщо частка а : b від’ємна, то числа а і b мають різні знаки, і навпаки;
– якщо частка а : b дорівнює нулю, то а дорівнює нулю, і навпаки.
Оскільки а ∙ 1 = а, то а : 1 = а для будь-якого а, і а : а = 1 для а ≠ 0.
Якщо число, відмінне від нуля, поділити на -1, то в частці дістанемо протилежне до нього число.
Наприклад, 5 : (-1) = -5.
Частка двох протилежних чисел, відмінних від нуля, дорівнює -1: – а : а = а : (-а) = -1 для а ≠ 0.
