ТЕМА : "Ділення на десятковий дріб"
Звернемо увагу на важливу властивість частки.
Розглянемо, наприклад, частку 16 : 8 = 2. Помножимо ділене і дільник, наприклад на 3. Маємо (16 ∙ 3) : (8 ∙ 3) = 48 : 24 = 2. Бачимо, що частка 16 : 8 не змінилася. Поділимо ділене й дільник частки 16 : 8 на 2. Маємо (16 : 2) : (8 : 2) = 8 : 4 = 2. Частка 16 : 8 знову не змінилася.
Звідси можна сформулювати правило, яке називають основною властивістю частки:
Якщо ділене й дільник помножити або поділити на одне й те саме натуральне число, то частка не зміниться.
Основна властивість частки дає змогу звести ділення на десятковий дріб до ділення на натуральне число.
Нехай треба поділити 35,56 на 1,4.
Основна властивість частки справджується також і для десяткових дробів.
Тому помножимо ділене й дільник на таке число, щоб дільник став натуральним числом. Таким множником буде 10, оскільки 1,4 ∙ 10 = 14. Отже, ділення на десятковий дріб можна звести до ділення на натуральне число: 35,56 : 1,4 = (35,56 ∙ 10) : (1,4 ∙ 10) = 355,6 : 14
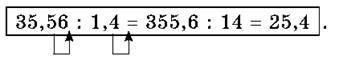
Міркуючи так, замість частки, наприклад, 1,215 : 0,45, знаходимо частку 121,5 : 45 = 2,7; замість частки 0,044 : 0,016 – частку 44 : 16 = 2,75 тощо.
У всіх випадках ділене й дільник множимо на розрядну одиницю 10, 100, 1000, …, а для цього досить перенести кому вправо на 1, 2 або 3 знаки.

Щоб поділити число на десятковий дріб, треба в діленому й дільнику перенести кому вправо на стільки цифр, скільки їх є в дільнику; після чого виконати ділення на натуральне число.
Якщо в діленому після коми менше цифр, ніж у дільнику, то до нього дописують потрібну кількість нулів.
Наприклад, 4,2 : 0,002 = 4200 : 2 = 2100.
Поділимо 3,748 на 0,1. Після перенесення коми на 1 знак вправо в діленому й дільнику маємо 3,748 : 0,1 = 37,48 : 1 = 37,48. Ще приклади:
4,973 : 0,01 = 497,3 : 1 = 497,3;
5,4 : 0,001 = 5400 : 1 = 5400.
Звідси маємо правило:
Щоб поділити десятковий дріб на 0,1; 0,01; 0,001; …, треба в цьому дробі перенести кому вправо на стільки знаків, скільки нулів містить дільник перед одиницею (враховуючи нуль цілих).

