ТЕМА "Середнє арифметичне, середнє значення величин"

Мабуть, читаючи книги та газети, різні статті в Інтернеті, дивлячись кіно й телевізійні передачі, ви чули таке: середня температура повітря за місяць чи за тиждень, середня швидкість автомобіля, середня народжуваність у місті Києві за 2011 рік, середній зріст учнів класу, середня успішність учнів 5-А класу за рік, середня врожайність помідорів тощо. Як же знаходять значення середніх величин? Для цього треба знати, що таке середнє арифметичне.

Подивіться на малюнок . Ви бачите на координатному промені точку А з координатою 3 і точку В з координатою 7. Між ними на однаковій відстані від обох точок знаходиться точка С з координатою 5. При цьому числа 3, 7 і 5 задовольняють таку числову рівність:

Кажуть, що число 5 є середнім арифметичним

Чисел 3 і 7. Щоб знайти середнє арифметичне двох чисел, треба знайти їх півсуму.

? Чи можна знайти середнє арифметичне трьох, чотирьох і більше чисел? Так.

Середнім арифметичним кількох чисел називається частка відділення суми цих чисел на їх кількість.

3адача. 

Знайдіть середнє арифметичне чисел 12,15 і 18.

Розв’язання. Задано 3 числа. Тому, щоб знайти їх середнє арифметичне, треба суму цих чисел поділити на 3:

? Чи може середнє арифметичну бути дробовим числом? Так. Наприклад:

Середнє арифметичне використовують для обчислення середніх величин. Розглянемо задачі.

Задача 2 . Під час подорожі автомобіль за першу годину проїхав 120 км, за другу годину – 110 км, а за третю і четверту – по 80 км. Скільки в середньому за годину проїжджав автомобіль?

Розв’язання. У задачі треба знайти середнє арифметичне чисел 

Отже, в середньому за годину автомобіль проїжджав 97,5 км.

Зверніть увагу:

Щоб знайти, скільки кілометрів у середньому долає за годину учасник руху, треба обчислити середнє арифметичне відстаней на різних ділянках руху.

Задача 3. На молокозавод привезли п’ять бідонів молока з різним відсотком жирності. У першому бідоні жирність молока становить 4 %, у другому – 3,8 %, у третьому – 3,5 %, у четвертому – 3,2 %, у п’ятому – 3,6 %. Яка середня жирність молока?

Розв’язання. Щоб знайти середню жирність молока, треба знайти середнє арифметичне заданих у задачі відсотків:

Отже, середня жирність молока становить 3,62 %.

Зверніть увагу:

Щоб знайти середній відсоток;, треба обчислити середнє арифметичне заданих відсотків.

ТЕМА "Знаходження числа за його відсотком"

ТЕМА : "Відсотки. Знаходження відсотків від даного числа"

Під час різних обчислень людям часто доводиться знаходити частини числа:  (половину),  (четвертину),  і т. д. 

ТЕМА : "Ділення на десятковий дріб"

Звернемо увагу на важливу властивість частки. 

Розглянемо, наприклад, частку 16 : 8 = 2. Помножимо ділене і дільник, наприклад на 3. Маємо (16 ∙ 3) : (8 ∙ 3) = 48 : 24 = 2. Бачимо, що частка 16 : 8 не змінилася. Поділимо ділене й дільник частки 16 : 8 на 2. Маємо (16 : 2) : (8 : 2) = 8 : 4 = 2. Частка 16 : 8 знову не змінилася. 

Звідси можна сформулювати правило, яке називають основною властивістю частки:

Якщо ділене й дільник помножити або поділити на одне й те саме натуральне число, то частка не зміниться.

Основна властивість частки дає змогу звести ділення на десятковий дріб до ділення на натуральне число.

Нехай треба поділити 35,56 на 1,4.

Основна властивість частки справджується також і для десяткових дробів.

Тому помножимо ділене й дільник на таке число, щоб дільник став натуральним числом. Таким множником буде 10, оскільки 1,4 ∙ 10 = 14. Отже, ділення на десятковий дріб можна звести до ділення на натуральне число: 35,56 : 1,4 = (35,56 ∙ 10) : (1,4 ∙ 10) = 355,6 : 14

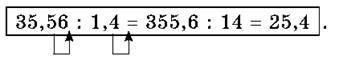
Міркуючи так, замість частки, наприклад, 1,215 : 0,45, знаходимо частку 121,5 : 45 = 2,7; замість частки 0,044 : 0,016 – частку 44 : 16 = 2,75 тощо.

У всіх випадках ділене й дільник множимо на розрядну одиницю 10, 100, 1000, …, а для цього досить перенести кому вправо на 1, 2 або 3 знаки. 

Щоб поділити число на десятковий дріб, треба в діленому й дільнику перенести кому вправо на стільки цифр, скільки їх є в дільнику; після чого виконати ділення на натуральне число.

Якщо в діленому після коми менше цифр, ніж у дільнику, то до нього дописують потрібну кількість нулів.

Наприклад, 4,2 : 0,002 = 4200 : 2 = 2100.

Поділимо 3,748 на 0,1. Після перенесення коми на 1 знак вправо в діленому й дільнику маємо 3,748 : 0,1 = 37,48 : 1 = 37,48. Ще приклади:

4,973 : 0,01 = 497,3 : 1 = 497,3;

5,4 : 0,001 = 5400 : 1 = 5400.

Звідси маємо правило:

Щоб поділити десятковий дріб на 0,1; 0,01; 0,001; …, треба в цьому дробі перенести кому вправо на стільки знаків, скільки нулів містить дільник перед одиницею (враховуючи нуль цілих).

ТЕМА : "Ділення десяткового дробу на натуральне число"

Щоб виконувати ділення десяткового дробу на десятковий, треба вміти виконувати ділення натуральних чисел і навчитися правильно визначати місце коми в отриманій частці. 

Спочатку розглянемо приклад, який допоможе сформулювати правило ділення десяткового дробу на натуральне число.

Задача. Довжина прямокутника дорівнює 15,6 дм, а ширина в 4 рази менша. Знайди ширину прямокутника.

Розв’язання. Щоб розв’язати задачу, виразимо довжину прямокутника в сантиметрах: 15,6 дм = 156 см. Маємо 156 : 4 = 39. Отже, ширина прямокутника 39 см, тобто 3,9 дм. Отже, 15,6 : 4 = 3,9.

Такий самий результат можна було отримати простіше, не перетворюючи дециметри в сантиметри.

Для цього потрібно поділити 15,6 на 4, не звертаючи уваги на кому, і поставити в частці кому, коли закінчиться ділення цілої частини.

Отже,

Щоб поділити десятковий дріб на натуральне число, потрібно:

1) поділити дріб на це число, не звертаючи уваги на кому, проте поставити в частці кому, коли закінчиться ділення цілої частини;

2) за потреби приписати справа після коми необхідну кількість нулів, щоб закінчити ділення.

Якщо ціла частина діленого менша від дільника, то в частці ставимо 0 цілих.

Приклад 1. Зверни увагу на те, що після ділення 28 на 5 отримали в частці 5 і остачу 3 десятих. Перетворили 3 десятих у 30 сотих (приписавши 0). Ділимо 30 сотих на 5, маємо в частці 6 сотих, а в остачі 0, ділення завершено.

За цим самим правилом можна виконувати ділення натуральних чисел, якщо ділення не виконується націло. 

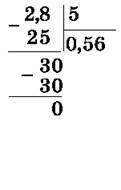
Приклад 2. 20 : 8 = 2,5.

За допомогою ділення можна знаходити десятковий дріб, що дорівнює даному звичайному дробу, тобто перетворювати звичайний дріб у десятковий.

Приклад 3. Перетвори дріб  у десятковий.

Розв’язання. 

Зважаючи, що 1,83 ∙ 10 = 18,3, тоді 18,3 : 10 = = 1,83. При діленні на 10 кому переносимо на одну цифру вліво. Оскільки 17,254 ∙ 100 = 1725,4, то 1725,4 : 100 = 17,254. При діленні на 100 кому переносимо на дві цифри вліво.

Узагальнюючи, маємо правило:

Щоб поділити десятковий дріб на 10, 100, 1000, …, треба в цьому дробі перенести кому вліво на стільки знаків, скільки нулів містить дільник.

Окремі випадки множення десяткових дробів

Часто доводиться множити десяткові дроби на числа, які містять одиницю і декілька нулів - чи то справа від одиниці, чи зліва.

           Щоб помножити десятковий дріб на 10, 100, 1000 і т.д., треба в цьому дробі перенести кому вправо відповідно на одну, дві, три і т.д. цифри.

          Приклад 1.  0,2658 · 100.

        Число 100 має 2 нулі, тому, щоб виконати задану дію, треба перенести кому в першому множнику на 2 цифри вправо:

0,2658 · 100 = 26,58.

 

         Приклад 2.   7,2 · 1000.

         Для виконання даного множення треба в числі 7,2 перенести кому на 3 цифри вправо. Але в цьому числі після коми лише одна цифра, тому дописуємо в ньому справа ще нулі:

7,2 · 1000 = 7,200 · 1000 = 7200.

 

          Щоб помножити десятковий дріб на   0,1,   0,01,   0,001 і т.д., треба перенести в цьому дробі кому на 1, 2, 3 і т.д. цифри вліво.

          Приклад 3.    4,5 · 0,001 = 0, 0045.

Множення десяткових дробів

Щоб помножити два десяткових дроби, треба перемножити їх, не беручи до уваги коми, а потім відділити комою у добутку стільки знаків, скільки їх стоїть справа після коми у двох множниках разом. Якщо в добутку буде менше цифр, ніж потрібно відокремити комою, то попереду дописують потрібну кількість нулів.

     Для множення десяткових дробів справджуються всі закони множення.

     Щоб помножити десятковий дріб на десять або сто, або тисячу тощо, потрібно в десятковому дробі кому перенести вправо на стільки знаків, скільки нулів стоїть після одиниці у множнику. Якщо десятковий дріб містить меншу кількість десяткових знаків, ніж та, на яку треба перенести кому, то справа від числа приписують необхідну кількість нулів.

    Наприклад:

Додавання і віднімання десяткових дробів

Віднімання десяткових дробів виконується порозрядно.

     Зручно це виконувати в стовпчик.

     При цьому десяткові дроби підписують одне під одним так, щоб кома була під комою. Віднімають десяткові дроби, як натуральні числа, не зважаючи на коми. У результаті кому ставлять під комами.

     Віднімаючи десяткові дроби з різною кількістю десяткових знаків, пам’ятайте, що цю кількість можна зрівняти, дописавши нулі в кінці числа.

     Для десяткових дробів справджуються властивості віднімання натуральних чисел.

 Наприклад:

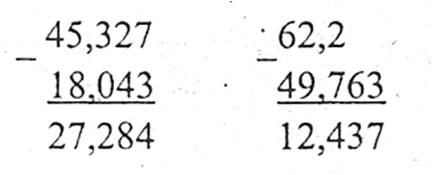
Додавання десяткових дробів виконується порозрядно.

     Зручно це виконувати в стовпчик.

     При цьому десяткові дроби підписують одне під одним так, щоб кома була під комою. Додають десяткові дроби, як натуральні числа, не зважаючи на коми. У результаті кому ставлять під комами.

     Додаючи десяткові дроби з різною кількістю десяткових знаків, пам’ятайте, що цю кількість можна зрівняти, дописавши нулі в кінці числа.

     Для десяткових дробів справджуються властивості додавання натуральних чисел.

    Наприклад:

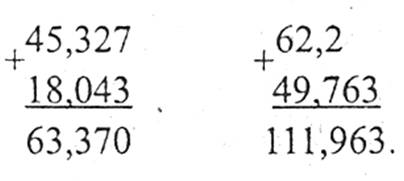
Округлення натуральних чисел і десяткових дробів

Припустимо, наприклад, що кількість учнів у школі на 1 вересня становить 1682. Однак через деякий час кількість учнів у школі зміниться, а тому назване число стане неправильним. У ньому зміниться цифра розрядів одиниць, а можливо, і десятків. Тому можна сказати, що в школі навчається приблизно 1680 учнів. Тобто ми замінили цифру одиниць на нуль. У цьому разі кажуть, що число округлили до десятків. Це записують так: 1682 ≈ 1680. Знак ≈ читається “наближено дорівнює”.

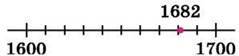
При округленні числа до заданого розряду необхідно, щоб округлене число якнайменше відрізнялося від заданого числа. Так, округлюючи 1682 до сотень, маємо 1682 ≈ 1700 (оскільки 1682 ближче до 1700, ніж до 1600) 

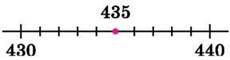
Нехай, наприклад, треба округлити до десятків число 435. Це особливий випадок, оскільки число 435 рівновіддалене від чисел 430 і 440 (рис. 256). У таких випадках домовилися округляти число “у більшу сторону”. Отже, 435 ≈ 440.

Маємо правило округлення натурального числа:

1) округлюючи натуральне число до певного розряду, всі цифри, що йдуть за ним, замінюють нулями;

2) якщо перша наступна за цим розрядом цифра 5, 6, 7, 8 або 9, то останню цифру, яка залишилася, збільшують на одиницю; якщо перша наступна за цим розрядом цифра 0, 1, 2, 3 або 4, то останню цифру, яка залишилася, не змінюють.

Приклад 1. Округли число 85 357 до тисяч.

Розв’язання. Підкреслимо цифру 5 у розряді тисяч: 85 357. Цифри, що стоять праворуч від неї (тобто 3, 5 та 7), замінюємо нулями. Наступна за розрядом тисяч є цифра 3, тому цифру тисяч 5 не змінюємо: 85 357 ≈ 85 000.

Відповідь: 85 000.

Приклад 2. Округли число 68 792 до найвищого розряду.

Розв’язання. Найвищим розрядом даного числа є десятки тисяч. Тому цифри 8, 7, 9 та 2 замінюємо нулями. Цифру в розряді десятків тисяч 6 збільшуємо на одиницю, оскільки наступна за нею цифра 8. Отже, записуємо так: 68 972 ≈ 70 000.

Відповідь: 70 000.

На практиці також часто виникає потреба округлити десяткові дроби. При цьому будемо користуватися тими самими правилами, що й для натуральних чисел.

Приклад 3. Округли число 82,2732 до десятих. Розв’язання. 82,2732 ≈ 82,3000. При цьому підкреслюємо цифру, що стоїть у розряді десятих. Цифри сотих, тисячних та десятитисячних замінюємо нулями, а цифру десятих збільшуємо на 1, оскільки наступною за нею є цифра 7. Проте 82,3000 = 82,3. Тому 82,2732 ≈ 82,3.

Приклад 4. Округли число 32,372 до сотих. Розв’язання. 32,372 ≈ 32,370. Підкреслюємо цифру, що стоїть у розряді сотих, цифру тисячних замінюємо нулем, а цифру сотих залишаємо без змін, оскільки наступною за нею є цифра 2. Проте 32,370 = 32,37. Тому 32,372 ≈ 32,37.

Приклад 5. Округли число 983,42 до десятків. Розв’язання. Якщо десятковий дріб округлюють до розряду, вищого за одиниці, то дробову частину відкидають, а цілу частину округлюють за правилом округлення натуральних чисел. Тому 983,42 ≈ 980. Отже, маємо правило округлення десяткового дробу:

Округлюючи десятковий дріб до певного розряду, 1) усі цифри, записані за цим розрядом, замінюємо нулями або відкидаємо (якщо вони стоять після коми); 2) якщо першою цифрою за цим розрядом є 0, 1, 2, 3 або 4, то останню цифру, що залишилася, не змінюємо; якщо першою цифрою за цим розрядом є 5, 6, 7, 8 або 9, то останню цифру, що залишилася, збільшуємо на 1.

Якщо при округленні десяткового дробу остання цифра, що залишилася в дробовій частині, буде 0, то відкидати її не можна (як ми це робимо з точними числами). У цьому разі цифра 0 наприкінці дробової частини показує, до якого розряду округлено число.

Порівняння десяткових дробів

Якщо до деякого десяткового дробу дописати праворуч нуль (або кілька нулів), то одержимо дріб, який дорівнює даному.

     Якщо деякий десятковий дріб закінчується нулями, то ці нулі можна відкинути й отримати дріб, який дорівнює даному.

     Серед двох десяткових дробів менший той дріб, у якого число цілих менше; і більший той, у якого число цілих більше.

     Щоб порівняти два десяткові дроби, треба спочатку порівняти цілі частини дробів; у разі їх рівності послідовно порівнюють десяті, якщо рівні десяті – порівнюють соті і т.д.

    Наприклад: 10,23>9,85; 3,759<3,81.

Десятковий дріб. Запис десяткових дробів

Нарівні зі звичайними дробами для запису дробових чисел використовують десяткові дроби.

Приклад 1. Виразимо відстань 7 дм 3 см у дециметрах.

Оскільки 

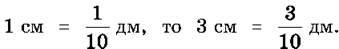
Тому

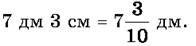
Приклад 2.

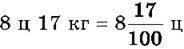
Знаменник дробової частини числа 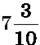 дорівнює 10, а числа 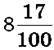дорівнює 100. Числа зі знаменниками 10, 100, 1000 … прийнято записувати без знаменника за допомогою  коми: спочатку пишуть цілу частину, а потім чисельник дробової частини; цілу частину відділяють від дробової частини комою. 

Наприклад, 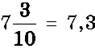 (читають: “7 цілих 3 десятих”),  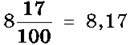(читають: “8 цілих 17 сотих”). 

Числа 7,3 і 8,17 – десяткові дроби. У вигляді десяткового дробу можна записати будь-яке число, знаменник дробової частини якого є одиницею з одним або кількома нулями. Цифри дробової частини ще називають десятковими знаками. У числа 8,17 два десяткових знаки: 1 і 7.

Якщо дріб правильний, то перед комою пишуть цифру 0.

Приклад 3.

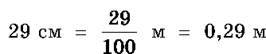
(читають: “0 цілих 29 сотих метра”).

Приклад 4. Виразимо 9 кг 71 г у кілограмах і запишемо десятковим дробом. Оскільки 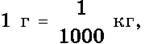 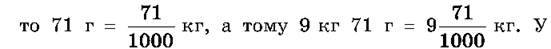 дробовій частині знайденого числа немає десятих частин кілограма (сотень грамів). Тому на першому місці після коми пишуть цифру  9,071 кг (читають: “9 цілих 71 тисячна кілограма”).

Отже, для того щоб записати звичайний дріб, знаменник дробової частини якого – розрядна одиниця 10, 100, 1000 … у вигляді десяткового дробу, 1) записують цілу частину числа (вона може дорівнювати 0) і ставлять кому;

2) справа від коми записують чисельник дробової частини, але він має містити стільки знаків, скільки нулів у знаменнику. Якщо в чисельнику менше знаків, ніж нулів у знаменнику, то після коми перед цифрами чисельника треба дописати таку кількість нулів, якої не вистачає.

Наприклад,

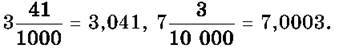
 Десяткові дроби записуються за таким самим принципом, що й натуральні числа в десятковій системі: кожна наступна одиниця, що стоїть праворуч, у 10 разів менша від попередньої. На першому місці після коми стоїть розряд десятих, на другому – розряд сотих, на третьому – розряд тисячних і т. д.

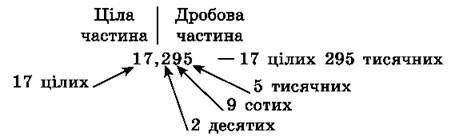
Десяткові дроби, як і звичайні, можна зображати на координатному промені. Наприклад, щоб на координатному промені зобразити десятковий дріб 0,6, спочатку запишемо його у вигляді звичайного дробу: 

 

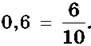
Потім поділимо одиничний відрізок на 10 рівних частин, кожна з яких становить 

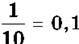  одиничного відрізка, і відкладемо від початку променя шість таких частин. Маємо точку А, що відповідає числу 0,6.

Щоб зобразити число 1,3, поділимо відрізок між числами 1 і 2 на десять рівних частин і відрахуємо 3 такі частини справа від числа 1. Маємо точку В, що відповідає числу 1,3.